

Next: НсЪјгя
Up: НтЮігыЪ§жЕМЦЫуЗНЗЈ
Previous: ЫцЛњЭјТчЕФМИКЮаджЪ
ЖдЦЋКУвРИНФЃаЭЕФвЛАуДІРэЗНЗЈАќКЌСЌајадЗНЗЈ[18,21]ЃЌЫйТЪЗНГЬ[20,23]ЃЌMasterЗНГЬ[19]гы
ЩњГЩКЏЪ§ЗНЗЈ[9]ЃЌетвВЪЧЭГМЦЮяРэбЇОГЃЪЙгУЕФЗНЗЈЁЃетвЛНкЃЌЮвУЧЮЇШЦЦЋКУвРИНФЃаЭЕФУнТЪЗжВМаЮЪННщЩмСЌајадЗНЗЈЃЌ
ЫйТЪЗНГЬгыMasterЗНГЬдкИДдгЭјТчбаОПжаЕФгІгУЁЃ
ПМТЧScale FreeЭјТчЕФЦЋКУвРИНФЃаЭЃЌДгЖЅЕуЕФЖШжЕБфЛЏЕФНЧЖШЃЌМйЩшЦфЖШжЕСЌајЃЌЮвУЧгаШчЯТЗНГЬЃЌ
УПвЛВНЮвУЧМгШыmЬѕБпЃЌМДдіМг2mИіЖШжЕЃЌгкЪЧ
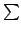 kj = 2mt + m0ЃЌдђ
kj = 2mt + m0ЃЌдђ
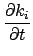 = = 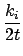
|
(29) |
ЖЅЕуkiЪЧдкtiЪБПЬНјШыЯЕЭГЕФЃЌЧвТњзуГѕЪМЬѕМў
ki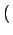 ti
ti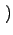 = mЃЌгкЪЧ
РћгУЩЯЪНЃЌНсКЯtiЕФЗжВМЃЌОЭПЩвджЊЕРШЮвтtЪБПЬkiЕФЗжВМЃЌМД
дкtЪБПЬЃЌ
ti
= mЃЌгкЪЧ
РћгУЩЯЪНЃЌНсКЯtiЕФЗжВМЃЌОЭПЩвджЊЕРШЮвтtЪБПЬkiЕФЗжВМЃЌМД
дкtЪБПЬЃЌ
ti 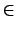
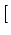 0, t
0, t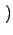 ЕФЗжВМКЏЪ§ЮЊ
ЕФЗжВМКЏЪ§ЮЊ
P(ti) = 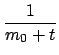 . .
|
(32) |
НсКЯвдЩЯСНЪНОЭПЩвдЕУЕНkiЕФЗжВМЃЌ
P(k) = 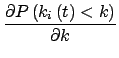 = = 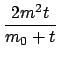 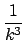 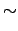 2m2k-3(t 2m2k-3(t 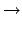 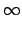 ). ).
|
(33) |
ЗНГЬ(28)ЪЧвЛжжЦНОљвтвхЩЯЕФУшЪіЃЌЪЕМЪЫцЛњЙ§ГЬжаЫљМгШыЕФБпжЛЪЧАДее
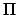
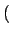 ki
ki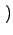 ЕФЗжВМРДбЁдёЃЌВЂВЛФмБЃ
жЄШЗЪЕШУУПвЛИіЖЅЕуЕФЖШжЕдіМгФЧУДДѓЃЌвВе§ЪЧвђДЫГЦЮЊСЌајадЗНЗЈЃЌЫљвдЖдЪЕМЪЫцЛњЙ§ГЬЗжВМКЏЪ§бнЛЏЕФУшЪіашвЊгУЕНЦфЫћЗНЗЈЁЃв§ШыЗжВМ
КЏЪ§
p
ЕФЗжВМРДбЁдёЃЌВЂВЛФмБЃ
жЄШЗЪЕШУУПвЛИіЖЅЕуЕФЖШжЕдіМгФЧУДДѓЃЌвВе§ЪЧвђДЫГЦЮЊСЌајадЗНЗЈЃЌЫљвдЖдЪЕМЪЫцЛњЙ§ГЬЗжВМКЏЪ§бнЛЏЕФУшЪіашвЊгУЕНЦфЫћЗНЗЈЁЃв§ШыЗжВМ
КЏЪ§
p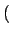 k;ti, t
k;ti, t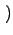 ЃЌБэЪОtiЪБПЬв§ШыЯЕЭГЕФЖЅЕудкtЪБПЬЖШжЕЮЊkЕФМИТЪЃЌЦфГѕЪМЬѕМўЮЊ
p
ЃЌБэЪОtiЪБПЬв§ШыЯЕЭГЕФЖЅЕудкtЪБПЬЖШжЕЮЊkЕФМИТЪЃЌЦфГѕЪМЬѕМўЮЊ
p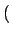 k;ti, ti
k;ti, ti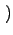 =
= 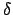
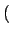 k - m
k - m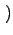 ЃЌЃЌТњзуШчЯТMasterЗНГЬЃЌ
ЃЌЃЌТњзуШчЯТMasterЗНГЬЃЌ
p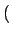 k;ti, t + 1 k;ti, t + 1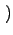 = p = p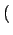 k;ti, t k;ti, t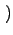 + wget + wget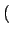 k - 1 k - 1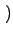 p p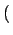 k - 1;ti, t k - 1;ti, t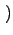 - wget - wget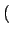 k - 1 k - 1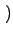 p p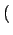 k;ti, t k;ti, t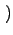
|
(34) |
Цфжа
wget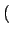 k
k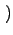 =
= 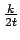 ЁЃЫљгаЖЅЕуЕФЖШжЕЗжВМЖЈвхЫљгаВЛЭЌЪБПЬМгШыЯЕЭГЕФЖЅЕуЕФЦНОљааЮЊЃЌМД
гавдЩЯСНЪНПЩвдЧѓЕУЖШЗжВМ
ЁЃЫљгаЖЅЕуЕФЖШжЕЗжВМЖЈвхЫљгаВЛЭЌЪБПЬМгШыЯЕЭГЕФЖЅЕуЕФЦНОљааЮЊЃЌМД
гавдЩЯСНЪНПЩвдЧѓЕУЖШЗжВМ
ЫйТЪЗНГЬДгСэвЛИіЗжВМПеМфУшЪіЁЃtЪБПЬЖШжЕЮЊkЕФЖЅЕузщГЩвЛИіМЏЭХЃЌМЏЭХДѓаЁЮЊ
Nk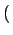 t
t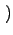 ЁЃЕБаТЖЅЕуНјШыЯЕЭГЪБЃЌ
NkПЩФмЗЂЩњИФБфЃЌЦфБфЛЏТЪТњзуШчЯТЗНГЬЃЌ
ЁЃЕБаТЖЅЕуНјШыЯЕЭГЪБЃЌ
NkПЩФмЗЂЩњИФБфЃЌЦфБфЛЏТЪТњзуШчЯТЗНГЬЃЌ
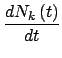 = mWget = mWget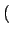 k - 1 k - 1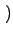 - mWget - mWget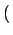 k k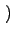 + + 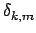 . .
|
(37) |
Цфжа
Wget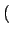 k
k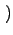 ЮЊЫљгаЖШжЕЮЊkЕФЖЅЕуЛёЕУаТЕФСЊНгЕФМИТЪЃЌ
NkЭЌбљТњзуЗНГЬ
ЮЊЫљгаЖШжЕЮЊkЕФЖЅЕуЛёЕУаТЕФСЊНгЕФМИТЪЃЌ
NkЭЌбљТњзуЗНГЬ
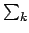 kNk
kNk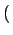 t
t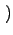 = 2mt + m0ЃЌЧв
НсКЯвЛЩЯЗНГЬПЩвдНтЕУЖШЗжВМ
P
= 2mt + m0ЃЌЧв
НсКЯвЛЩЯЗНГЬПЩвдНтЕУЖШЗжВМ
P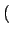 k
k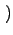 ЃЌОпЬхМЦЫуМћЮФеТ[20,23]ЁЃ
ЃЌОпЬхМЦЫуМћЮФеТ[20,23]ЁЃ


Next: НсЪјгя
Up: НтЮігыЪ§жЕМЦЫуЗНЗЈ
Previous: ЫцЛњЭјТчЕФМИКЮаджЪ
wwwwjs
2004-01-04
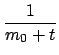 .
.
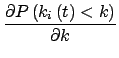 =
= 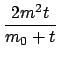
![]()
![]() ki
ki![]() ЕФЗжВМРДбЁдёЃЌВЂВЛФмБЃ
жЄШЗЪЕШУУПвЛИіЖЅЕуЕФЖШжЕдіМгФЧУДДѓЃЌвВе§ЪЧвђДЫГЦЮЊСЌајадЗНЗЈЃЌЫљвдЖдЪЕМЪЫцЛњЙ§ГЬЗжВМКЏЪ§бнЛЏЕФУшЪіашвЊгУЕНЦфЫћЗНЗЈЁЃв§ШыЗжВМ
КЏЪ§
p
ЕФЗжВМРДбЁдёЃЌВЂВЛФмБЃ
жЄШЗЪЕШУУПвЛИіЖЅЕуЕФЖШжЕдіМгФЧУДДѓЃЌвВе§ЪЧвђДЫГЦЮЊСЌајадЗНЗЈЃЌЫљвдЖдЪЕМЪЫцЛњЙ§ГЬЗжВМКЏЪ§бнЛЏЕФУшЪіашвЊгУЕНЦфЫћЗНЗЈЁЃв§ШыЗжВМ
КЏЪ§
p![]() k;ti, t
k;ti, t![]() ЃЌБэЪОtiЪБПЬв§ШыЯЕЭГЕФЖЅЕудкtЪБПЬЖШжЕЮЊkЕФМИТЪЃЌЦфГѕЪМЬѕМўЮЊ
p
ЃЌБэЪОtiЪБПЬв§ШыЯЕЭГЕФЖЅЕудкtЪБПЬЖШжЕЮЊkЕФМИТЪЃЌЦфГѕЪМЬѕМўЮЊ
p![]() k;ti, ti
k;ti, ti![]() =
= ![]()
![]() k - m
k - m![]() ЃЌЃЌТњзуШчЯТMasterЗНГЬЃЌ
ЃЌЃЌТњзуШчЯТMasterЗНГЬЃЌ
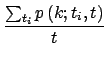 .
.
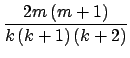
![]() t
t![]() ЁЃЕБаТЖЅЕуНјШыЯЕЭГЪБЃЌ
NkПЩФмЗЂЩњИФБфЃЌЦфБфЛЏТЪТњзуШчЯТЗНГЬЃЌ
ЁЃЕБаТЖЅЕуНјШыЯЕЭГЪБЃЌ
NkПЩФмЗЂЩњИФБфЃЌЦфБфЛЏТЪТњзуШчЯТЗНГЬЃЌ
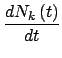 = mWget
= mWget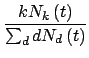 .
.
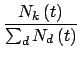 .
.