ΆΦ¬έ”κΗ≈¬ ¬έ «Άχ¬γ―–ΨΩΒΡ÷Ί“ΣΙΛΨΏΓΘ‘ΎΥφΜζΆχ¬γΡΘ–Ά“ΜΫΎΘ§Έ“Ο«“―Ψ≠ΝΥΫβΘ§ΑϋΚ§nΗωΕΞΒψΒΡΥφΜζΆχ¬γ”–ΝΫ÷÷
G![]() n, M
n, M![]() ”κ
G
”κ
G![]() n, p
n, p![]() ΓΘœ÷‘ΎΈ“Ο«”Ο’βΝΫ÷÷Άχ¬γΖ÷±πΙΙ‘λΝΫΗωΗ≈¬ Ω’ΦδΓΘΦ«
N = C2nȧ
G
ΓΘœ÷‘ΎΈ“Ο«”Ο’βΝΫ÷÷Άχ¬γΖ÷±πΙΙ‘λΝΫΗωΗ≈¬ Ω’ΦδΓΘΦ«
N = C2nȧ
G![]() n, M
n, M![]() ΑϋΚ§ΝΥCMN
ΗωΩ…ΡήΒΡΆχ¬γΘ§ΦΌ…ηΥυ”–ΒΡΆχ¬γΒ»ΦΗ¬ Θ§‘ρ
G
ΑϋΚ§ΝΥCMN
ΗωΩ…ΡήΒΡΆχ¬γΘ§ΦΌ…ηΥυ”–ΒΡΆχ¬γΒ»ΦΗ¬ Θ§‘ρ
G![]() n, M
n, M![]() ≥…ΈΣΗ≈¬ Ω’ΦδΓΘΗχΕ®Άχ¬γ
H
≥…ΈΣΗ≈¬ Ω’ΦδΓΘΗχΕ®Άχ¬γ
H ![]() G
G![]() n, M
n, M![]() ΒΡΦΗ¬ ΈΣ
ΒΡΦΗ¬ ΈΣ
| P(GM = H) = (CMN)-1. | (23) |
Ε‘”ΎΥφΜζΆχ¬γ
G![]() n, p
n, p![]() Θ§ ΒΦ …œΥϋΑϋΚ§ΝΥ2NΗωΥυ”–Ω…ΡήΒΡΆχ¬γΘ§¥”Ω’ΆΦΒΫΆξ»ΪΆΦΓΘΦ«
e
Θ§ ΒΦ …œΥϋΑϋΚ§ΝΥ2NΗωΥυ”–Ω…ΡήΒΡΆχ¬γΘ§¥”Ω’ΆΦΒΫΆξ»ΪΆΦΓΘΦ«
e![]() H
H![]() ΈΣΆχ¬γHΒΡ±Ώ ΐΘ§
ΗχΕ®Άχ¬γ
H
ΈΣΆχ¬γHΒΡ±Ώ ΐΘ§
ΗχΕ®Άχ¬γ
H ![]() G
G![]() n, p
n, p![]() ΒΡΦΗ¬ ΈΣ
ΒΡΦΗ¬ ΈΣ
|
P(Gp = H) = pe |
(24) |
¥”Ά≥ΦΤΈοάμ―ßœΒΉέάμ¬έΒΡΫ«Ε»Έ“Ο«Ω…“‘’β―υά¥Ω¥Η≈¬ Ω’Φδ
G![]() n, p
n, p![]() ΓΘΈ“Ο«Α―
e
ΓΘΈ“Ο«Α―
e![]() H
H![]() Ω¥ΉςΆΦHΒΡΚξΙέΝΩΘ§άύ±»”Ύ
ΈοάμœΒΆ≥ΈΔΙέΉ¥Χ§ΒΡΡήΝΩΘ§Η≈¬ Ω’Φδ
G
Ω¥ΉςΆΦHΒΡΚξΙέΝΩΘ§άύ±»”Ύ
ΈοάμœΒΆ≥ΈΔΙέΉ¥Χ§ΒΡΡήΝΩΘ§Η≈¬ Ω’Φδ
G![]() n, p
n, p![]() ΙΊ”ΎeΒΡΖ÷≤ΦΈΣ
ΙΊ”ΎeΒΡΖ÷≤ΦΈΣ
‘ΎΉιΚœœΒ ΐCeN…œΘ§ΆΦ¬έ”κΆ≥ΦΤΈοάμ―ß”–≤ΜΆ§ΒΡ¥ΠάμΖΫ ΫΓΘΆΦ¬έΕ®“εΝΥΆΦΒΡΆ§Χ§ΙΊœΒ--»γΙϊΆΦ
V![]() G1
G1![]() ”κ
V
”κ
V![]() G2
G2![]() ÷°Φδ¥φ‘ΎΩ…Ρφ”≥…δ
÷°Φδ¥φ‘ΎΩ…Ρφ”≥…δ
![]() : V
: V![]() G1
G1![]()
![]() V
V![]() G2
G2![]() Θ§ ΙΒΟΕ‘”Ύ
Θ§ ΙΒΟΕ‘”Ύ
![]() x, y
x, y ![]() V
V![]() G1
G1![]() Θ§
»γΙϊ
xy
Θ§
»γΙϊ
xy ![]() E
E![]() G1
G1![]() ‘ρ
‘ρ
![]()
![]() x
x![]()
![]()
![]() y
y![]()
![]() E
E![]() G2
G2![]() ΓΘΥυ“‘ΗχΕ®ΆΦHœύΒ±”ΎΗχΕ®ΝΥH
“‘ΦΑ”κHΆ§Χ§ΒΡΥυ”–ΆΦΓΘ¥”Ά≥ΦΤΈοάμ―ßά¥Ω¥Θ§’βœύΒ±”ΎΕΞΒψ≤ΜΩ…«χΖ÷ΒΡ«ιΩωΘ§’β ±ΚρΆχ¬γΫαΙΙ≥…ΈΣ≤ΜΆ§Άχ¬γΒΡΈ®“Μ«χ±πΘ§Ά§Χ§ΆΦΨΆ»γΆ§ΈΔΙέ
Ή¥Χ§ΒΡΦρ≤ΔΕ»ΓΘΒΪ «Ε‘”ΎΕΞΒψΩ…«χΖ÷ΒΡΆχ¬γΘ§‘ΎΆχ¬γΫαΙΙœύΆ§ΒΡ«ιΩωœ¬Θ§œύΆ§ΒΡΝ§ΫαΖΫ ΫΝ§‘Ύ≤ΜΆ§ΕΞΒψ…œ»‘»Μ”–÷ΒΒΟ«χΖ÷ΒΡ“β“εΓΘ”…”ΎΡΩ«Α
―–ΨΩΒΡ ΒΦ œΒΆ≥ΕΞΒψΕΦ «Ω…“‘«χΖ÷ΒΡΘ§Έ“Ο«≤ΜΩΦ¬«Άχ¬γΒΡΆ§Χ§ΓΘ
ΓΘΥυ“‘ΗχΕ®ΆΦHœύΒ±”ΎΗχΕ®ΝΥH
“‘ΦΑ”κHΆ§Χ§ΒΡΥυ”–ΆΦΓΘ¥”Ά≥ΦΤΈοάμ―ßά¥Ω¥Θ§’βœύΒ±”ΎΕΞΒψ≤ΜΩ…«χΖ÷ΒΡ«ιΩωΘ§’β ±ΚρΆχ¬γΫαΙΙ≥…ΈΣ≤ΜΆ§Άχ¬γΒΡΈ®“Μ«χ±πΘ§Ά§Χ§ΆΦΨΆ»γΆ§ΈΔΙέ
Ή¥Χ§ΒΡΦρ≤ΔΕ»ΓΘΒΪ «Ε‘”ΎΕΞΒψΩ…«χΖ÷ΒΡΆχ¬γΘ§‘ΎΆχ¬γΫαΙΙœύΆ§ΒΡ«ιΩωœ¬Θ§œύΆ§ΒΡΝ§ΫαΖΫ ΫΝ§‘Ύ≤ΜΆ§ΕΞΒψ…œ»‘»Μ”–÷ΒΒΟ«χΖ÷ΒΡ“β“εΓΘ”…”ΎΡΩ«Α
―–ΨΩΒΡ ΒΦ œΒΆ≥ΕΞΒψΕΦ «Ω…“‘«χΖ÷ΒΡΘ§Έ“Ο«≤ΜΩΦ¬«Άχ¬γΒΡΆ§Χ§ΓΘ
Β±Έ“Ο«ΥΒΥφΜζΆΦ
G![]() n, p
n, p![]() ΨΏ”––‘÷ Q÷ΗΒΡ «‘ΎΥφΜζΆΦΒΡΗ≈¬ Ω’Φδ÷–Θ§¥”ΤΫΨυ“β“ε…œ”––‘÷ QΓΘœ÷‘ΎΈ“Ο«Χ÷¬έΥφΜζΆχ¬γ
ΕΞΒψΒΡΕ»÷ΒΖ÷≤ΦΓΘΈ“Ο« Ήœ»Ε‘”ΎΟΩ“ΜΗωΈΔΙέΆΦΆ≥ΦΤΤδΕΞΒψΕ»÷ΒΖ÷≤ΦΙφ¬…Θ§»ΜΚσΑ¥’’≤ΜΆ§ΈΔΙέΆΦ≥ωœ÷ΒΡΦΗ¬ Ήω“ΜΗωΤΫΨυΘ§ΨΆΩ…“‘ΫβΨω’βΗωΈ ΧβΓΘ
ΒΪ «Θ§Φ¥ ΙΕ‘”ΎΈΔ’ΐ‘ρœΒΉέ
G
ΨΏ”––‘÷ Q÷ΗΒΡ «‘ΎΥφΜζΆΦΒΡΗ≈¬ Ω’Φδ÷–Θ§¥”ΤΫΨυ“β“ε…œ”––‘÷ QΓΘœ÷‘ΎΈ“Ο«Χ÷¬έΥφΜζΆχ¬γ
ΕΞΒψΒΡΕ»÷ΒΖ÷≤ΦΓΘΈ“Ο« Ήœ»Ε‘”ΎΟΩ“ΜΗωΈΔΙέΆΦΆ≥ΦΤΤδΕΞΒψΕ»÷ΒΖ÷≤ΦΙφ¬…Θ§»ΜΚσΑ¥’’≤ΜΆ§ΈΔΙέΆΦ≥ωœ÷ΒΡΦΗ¬ Ήω“ΜΗωΤΫΨυΘ§ΨΆΩ…“‘ΫβΨω’βΗωΈ ΧβΓΘ
ΒΪ «Θ§Φ¥ ΙΕ‘”ΎΈΔ’ΐ‘ρœΒΉέ
G![]() n, e
n, e![]() ÷–ΒΡ―υ±ΨΒψ“≤¥φ‘Ύ≤ΜΆ§ΒΡΕ»÷ΒΖ÷≤Φ–Έ ΫΘ§“ρΕχ ΒΦ …œ Βœ÷’β“ΜΖΫΖ®≤Δ≤ΜΦρΒΞΓΘœ÷‘ΎΈ“Ο«ΜΜ“ΜΗωΫϋΥΤΒΡ
ΖΫΖ®ΓΘ”…’ΐ‘ρœΒΉέΖ÷≤ΦΚ· ΐ(25) ΫΩ…ΦϊΘ§Ζ÷≤ΦΚ· ΐΒΡΉν¥σ÷ΒΒψ «±Ώ ΐΒΡΤΫΨυ÷Β
÷–ΒΡ―υ±ΨΒψ“≤¥φ‘Ύ≤ΜΆ§ΒΡΕ»÷ΒΖ÷≤Φ–Έ ΫΘ§“ρΕχ ΒΦ …œ Βœ÷’β“ΜΖΫΖ®≤Δ≤ΜΦρΒΞΓΘœ÷‘ΎΈ“Ο«ΜΜ“ΜΗωΫϋΥΤΒΡ
ΖΫΖ®ΓΘ”…’ΐ‘ρœΒΉέΖ÷≤ΦΚ· ΐ(25) ΫΩ…ΦϊΘ§Ζ÷≤ΦΚ· ΐΒΡΉν¥σ÷ΒΒψ «±Ώ ΐΒΡΤΫΨυ÷Β
![]() = NpΘ§«“ΕΰœνΖ÷≤ΦΥΞΦθΒΡΖ«≥ΘΩλΘ§“ρ¥ΥΘ§Έ“Ο«
Ω…“‘≥Δ ‘‘ΎΖ÷≤ΦΚ· ΐΖε÷ΒΗΫΫϋΒΡΈΔΙέΆΦ…œΉνΫϋΥΤΒΡΤΫΨυΓΘ’β―υΘ§Έ ΧβΨΆ±δ≥…ΈΔ’ΐ‘ρœΒΉέΥφΜζΆΦ
G
= NpΘ§«“ΕΰœνΖ÷≤ΦΥΞΦθΒΡΖ«≥ΘΩλΘ§“ρ¥ΥΘ§Έ“Ο«
Ω…“‘≥Δ ‘‘ΎΖ÷≤ΦΚ· ΐΖε÷ΒΗΫΫϋΒΡΈΔΙέΆΦ…œΉνΫϋΥΤΒΡΤΫΨυΓΘ’β―υΘ§Έ ΧβΨΆ±δ≥…ΈΔ’ΐ‘ρœΒΉέΥφΜζΆΦ
G![]() n, Np
n, Np![]() ΒΡΕ»÷ΒΖ÷≤Φ–Έ ΫΓΘ
ΒΡΕ»÷ΒΖ÷≤Φ–Έ ΫΓΘ
÷Ί–¬±μ ωΈ Χβ»γœ¬ΘΚ‘ΎnΗωΕΞΒψΒΡΆχ¬γ÷–Β»ΦΗ¬ ΒΊ―Γ»Γ
![]() n(n - 1)pΧθ±ΏΘ§«σΤΫΨυ“β“ε…œΕΞΒψ±Μ―ûåΈ ΐΒΡΖ÷≤Φ–Έ ΫΓΘ Ήœ»Θ§Έ“Ο«ά¥Ω¥Ρ≥
“ΜΗωΕΞΒψ±Μ―Γ»ΓΒΡΦΗ¬
n(n - 1)pΧθ±ΏΘ§«σΤΫΨυ“β“ε…œΕΞΒψ±Μ―ûåΈ ΐΒΡΖ÷≤Φ–Έ ΫΓΘ Ήœ»Θ§Έ“Ο«ά¥Ω¥Ρ≥
“ΜΗωΕΞΒψ±Μ―Γ»ΓΒΡΦΗ¬ ![]() ΓΘ‘ΎΒΎ“ΜΧθ±ΏΒΡ―Γ»ΓΒΡ ±ΚρΘ§ΟΩ“ΜΗωΕΞΒψΨΏ”–(n - 1)ΧθΩ…“‘±Μ―Γ»ΓΒΡ±ΏΘ§±Μ―Γ»ΓΒΡΦΗ¬ œύΆ§Θ§”÷“ρΈΣΟΩ―Γ»Γ
“ΜΧθ±Ώ≤ζ…ζΝΫΗωΕΞΒψΘ§Υυ“‘»Έ“ΜΕΞΒψ±Μ―Γ»ΓΒΡΦΗ¬
ΓΘ‘ΎΒΎ“ΜΧθ±ΏΒΡ―Γ»ΓΒΡ ±ΚρΘ§ΟΩ“ΜΗωΕΞΒψΨΏ”–(n - 1)ΧθΩ…“‘±Μ―Γ»ΓΒΡ±ΏΘ§±Μ―Γ»ΓΒΡΦΗ¬ œύΆ§Θ§”÷“ρΈΣΟΩ―Γ»Γ
“ΜΧθ±Ώ≤ζ…ζΝΫΗωΕΞΒψΘ§Υυ“‘»Έ“ΜΕΞΒψ±Μ―Γ»ΓΒΡΦΗ¬
![]() =
= ![]() ΓΘΦΌ…ηp
ΓΘΦΌ…ηp ![]() 1Θ§‘ρ±Μ―Γ»ΓΒΡ±Ώ≤Δ≤Μ”Αœλ”κΤδΙΊΝΣΒΡΕΞΒψ‘Ό¥Έ±Μ―Γ
»ΓΒΡΦΗ¬ ΓΘ“ρ¥ΥΦΗ¬ ΈΣ
1Θ§‘ρ±Μ―Γ»ΓΒΡ±Ώ≤Δ≤Μ”Αœλ”κΤδΙΊΝΣΒΡΕΞΒψ‘Ό¥Έ±Μ―Γ
»ΓΒΡΦΗ¬ ΓΘ“ρ¥ΥΦΗ¬ ΈΣ![]() ΒΡΕΞΒψ±Μ―Γ»ΓΒΡΫϋΕάΝΔ ¬ΦΰΙΙ≥…Η≈¬ Ω’ΦδΘ§ΤδΖ÷≤ΦΖϊΚœΤΫΨυ÷ΒΈΣ
ΒΡΕΞΒψ±Μ―Γ»ΓΒΡΫϋΕάΝΔ ¬ΦΰΙΙ≥…Η≈¬ Ω’ΦδΘ§ΤδΖ÷≤ΦΖϊΚœΤΫΨυ÷ΒΈΣ
![]() =
= ![]() x
x ![]() n(n - 1)p = (n - 1)p
n(n - 1)p = (n - 1)p ![]() np
ΒΡ≤¥Υ…Ζ÷≤ΦΘ§Φ¥
np
ΒΡ≤¥Υ…Ζ÷≤ΦΘ§Φ¥
“ΜΗωΗϋ”–Έοάμ―ßΖγΗώΒΡΖΫΖ®[1] «ΦΤΥψ‘ΎΥφΜζΆΦ
G![]() n, p
n, p![]() ÷–Θ§“ΜΗωΕΞΒψΩ…Ρή”–ΒΡΥυ”–ΝΣΫ” ΐΘ§ΨΓΙή¥ΥΝΣΫ” ΐ≤Μ“ΜΕ® «Ρ≥ΗωΆχ¬γ÷–ΥϋΒΡΕ»÷Β
ΒΡΚ§“εΘ§
÷–Θ§“ΜΗωΕΞΒψΩ…Ρή”–ΒΡΥυ”–ΝΣΫ” ΐΘ§ΨΓΙή¥ΥΝΣΫ” ΐ≤Μ“ΜΕ® «Ρ≥ΗωΆχ¬γ÷–ΥϋΒΡΕ»÷Β
ΒΡΚ§“εΘ§
| P(ki = k) = Ckn-1pk(1 - p)n-1-k. | (27) |
Β±»ΜΘ§ΫβΨωΕ»Ζ÷≤ΦΈ ΧβΗϋΦ”÷±ΫΊΝΥΒ±ΒΡΖΫ Ϋ «≤ζ…ζΉψΙΜΕύΒΡΥφΜζΆΦ―υ±ΨΒψΘ§»ΜΚσΫχ––Ά≥ΦΤΓΘΑ¥’’ΕΰœνΖ÷≤ΦΒΡΦβΖεΧΊ’ςΘ§÷Μ“Σ…ΌΝΩΒΡ―υ±ΨΨΆΩ…“‘ ΒΟΒΫ±»ΫœΉΦ»ΖΒΡΆχ¬γ–‘÷ ΓΘΦϊΆΦ(5)Θ§ΆΦ÷–÷Μ”ΟΝΥ“ΜΗωΈΔΙέΆΦά¥ΦΤΥψΓΘΒ±Έ“Ο« ΒΦ ΡΟΒΫ“ΜΗωΆχ¬γΒΡ ΐΨίΫχ––Ζ÷Έω ±Θ§“ΜΑψΈ“Ο«÷±Ϋ” ‘Ύ’βΗωΆχ¬γ…œΆ≥ΦΤ–‘÷ Q «Ζώ¥φ‘ΎΘ§Κή…Ό–η“Σ¥σΝΩΒΡΆ§÷ Άχ¬γΉι≥…œΒΉέά¥Χ÷¬έΓΘ’β”κΆ≥ΦΤΈοάμ÷– ΒΦ ≤βΝΩ“ΜΗωœΒΆ≥ «“Μ―υΒΡΓΘΈ“Ο«ΒΡάμ¬έ « Ϋ®ΝΔ‘ΎΚξΙέΉ¥Χ§”κΈΔΙέΉ¥Χ§ΒΡΙΊœΒΒΡΜυ¥Γ…œΒΡΘ§ΒΪ «Ε‘”Ύ ΒΦ ≤βΝΩΘ§Έ“Ο«“≤÷Μ–η“Σ“ΜΗωœΒΆ≥ΨΆΩ…“‘ΝΥΓΘ
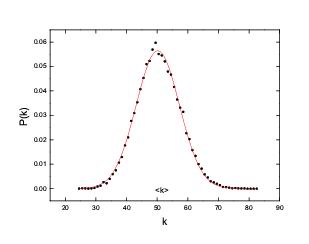
ΥφΜζΆχ¬γ―–ΨΩΒΡΝμ“ΜΗω÷Ί“ΣΖΫΟφ «”κΆ≥ΦΤΈοάμ―ßΝΣœΒ‘Ύ“ΜΤπΒΡœύ±δœ÷œσΘ§’β“≤ «ΥφΜζΆχ¬γΒΟΒΫ≥δΖ÷―–ΨΩΒΡ‘≠“ρ÷°“ΜΓΘΥφΜζΆχ¬γΒΡœύ±δœ÷œσ±μœ÷
ΈΣΦΗΚΈ–‘÷ ΥφΉ≈≤Έ ΐpΒΡΆΜœ÷–‘Θ§¥φ‘ΎΚήΕύΒΡΦΗΚΈ–‘÷ Q÷Μ”–Β±
p > pQc≤≈Μα≥ωœ÷Θ§’Ιœ÷≥ωάύΥΤ”ΎΕΰΦΕœύ±δΒΡ––ΈΣΓΘάΐ»γΈ“Ο«Χ÷¬έΆχ¬γ
Ήν¥σΦ·Ά≈ΒΡœύΕ‘¥σ–ΓΓΘΆΦΒΡ“ΜΗωΝ§Ά®Ή”ΆΦ≥ΤΈΣΆΦΒΡΦ·Ά≈Θ§Τδ÷–ΕΞΒψ ΐΉνΕύΒΡ≥ΤΈΣΉν¥σΦ·Ά≈ΓΘΥυ―–ΨΩΒΡΈ Χβ «p÷ΒΕ‘Άχ¬γΉν¥σΦ·Ά≈œύΕ‘”Ύ’ϊ
ΗωΆχ¬γΒΡœύΕ‘¥σ–ΓΒΡ”ΑœλΓΘΦ«Ήν¥σΦ·Ά≈¥σ–ΓΈΣSΘ§ΤδœύΕ‘¥σ–ΓΈΣ
s = ![]() ΓΘΩ…“‘Ω¥ΒΫΘ§»γΙϊ
p
ΓΘΩ…“‘Ω¥ΒΫΘ§»γΙϊ
p ![]() 1‘ρΘ§Ήν¥σΦ·Ά≈”κ’ϊΗωΆχ¬γ
¥σ–ΓœύΒ±Θ§Εχ
p
1‘ρΘ§Ήν¥σΦ·Ά≈”κ’ϊΗωΆχ¬γ
¥σ–ΓœύΒ±Θ§Εχ
p ![]() 0‘ρœύΖ¥ΓΘΡ«Ο¥Θ§0 < p < 1ΒΡ«ιΩωΡΊΘΩ’β‘ΎΥφΜζΆχ¬γΒΡ―–ΨΩ÷–±Μ≥ΤΈΣΆχ¬γΒΡ―ίΜ·–‘÷ ΓΘ
0‘ρœύΖ¥ΓΘΡ«Ο¥Θ§0 < p < 1ΒΡ«ιΩωΡΊΘΩ’β‘ΎΥφΜζΆχ¬γΒΡ―–ΨΩ÷–±Μ≥ΤΈΣΆχ¬γΒΡ―ίΜ·–‘÷ ΓΘ
―–ΨΩ’β–©Έ Χβ“Σ”ΟΒΫΥφΜζΆΦ―ίΜ·–ρΝ–ΙΙ≥…ΒΡΗ≈¬ Ω’Φδ
![]() Θ§Ε®“εΈΣ¥”Ω’ΆΦΒΫΆξ»ΪΆΦΒΡΥφΜζΆΦ–ρΝ–
Θ§Ε®“εΈΣ¥”Ω’ΆΦΒΫΆξ»ΪΆΦΒΡΥφΜζΆΦ–ρΝ–
![]() : = G
: = G![]() n, 0
n, 0![]() , G
, G![]() n, 1
n, 1![]() ,..., G
,..., G![]() n, N
n, N![]() Ήι≥…ΒΡΒ»ΦΗ¬ Ω’ΦδΘ§Τδ÷–
G
Ήι≥…ΒΡΒ»ΦΗ¬ Ω’ΦδΘ§Τδ÷–
G![]() n, t
n, t![]() ±μ Ψt ±
ΩΧΒΡΆΦΘ§“≤±μ Ψ”–tΧθ±ΏΒΡΆΦΓΘΒ±
n
±μ Ψt ±
ΩΧΒΡΆΦΘ§“≤±μ Ψ”–tΧθ±ΏΒΡΆΦΓΘΒ±
n ![]()
![]() ±’βΗωΩ’ΦδΩ…“‘Ω¥≥… «”…ΗςΗω
G
±’βΗωΩ’ΦδΩ…“‘Ω¥≥… «”…ΗςΗω
G![]() n, M
n, M![]() Ω’Φδ÷–ΉιΚœΕχ≥…Θ§Μρ’ΏΩ¥≥…”…≤Μ
Ά§p÷ΒΒΡ
G
Ω’Φδ÷–ΉιΚœΕχ≥…Θ§Μρ’ΏΩ¥≥…”…≤Μ
Ά§p÷ΒΒΡ
G![]() n, p
n, p![]() Ω’ΦδΉιΚœΕχ≥…ΒΡΩ’ΦδΓΘΙΊ”ΎsΒΡΈ ΧβΨΆΩ…“‘‘Ύ’β―υΒΡΗ≈¬ Ω’Φδ÷–ΒΟΒΫ―–ΨΩΓΘΫαΙϊ±μΟςΕ‘”ΎΉν¥σΦ·Ά≈Θ§
Β±
p < psc =
Ω’ΦδΉιΚœΕχ≥…ΒΡΩ’ΦδΓΘΙΊ”ΎsΒΡΈ ΧβΨΆΩ…“‘‘Ύ’β―υΒΡΗ≈¬ Ω’Φδ÷–ΒΟΒΫ―–ΨΩΓΘΫαΙϊ±μΟςΕ‘”ΎΉν¥σΦ·Ά≈Θ§
Β±
p < psc = ![]() ±≤Μ¥φ‘Ύ¥σΙφΡΘΦ·Ά≈Θ§Β±
p = psc =
±≤Μ¥φ‘Ύ¥σΙφΡΘΦ·Ά≈Θ§Β±
p = psc = ![]() ±Θ§Ήν¥σΦ·Ά≈¥σ–ΓΈΣ
S
±Θ§Ήν¥σΦ·Ά≈¥σ–ΓΈΣ
S ![]() n
n![]() Θ§Β±
p > psc =
Θ§Β±
p > psc = ![]() ±Ήν¥σΦ·Ά≈¥σ–ΓS
±Ήν¥σΦ·Ά≈¥σ–ΓS ![]() nΓΘ
nΓΘ
λœΛΆ≥ΦΤΈοάμ…χΝςάμ¬έΒΡΜΑΨΆΜαΚή»ί“ΉΖΔœ÷’β÷÷œ÷œσ”κ…χΝςάμ¬έΒΡΝΣœΒΓΘ ΒΦ …œΥϊΟ«±Ψά¥ΨΆ «Ά§“ΜΦΰ ¬«ιΘ§÷Μ≤ΜΙΐ¥”≤ΜΆ§ΒΡΫ«Ε»Ϋχ––―–ΨΩΓΘάΐ »γΈ“Ο«÷ΣΒάΘ§‘Ύ…χΝςΈ Χβ÷–Θ§‘Ύp = pcΗΫΫϋΘ§ΗςΝ§Ά®Φ·Ά≈ΒΡΙφΡΘ’Ιœ÷Οί¬ Ζ÷≤ΦΓΘΆ§―υΘ§‘ΎΥφΜζΆχ¬γ÷–Θ§“≤¥φ‘Ύ’β÷÷Οί¬…–Έ ΫΒΡΙφΡΘΖ÷≤ΦΓΘ